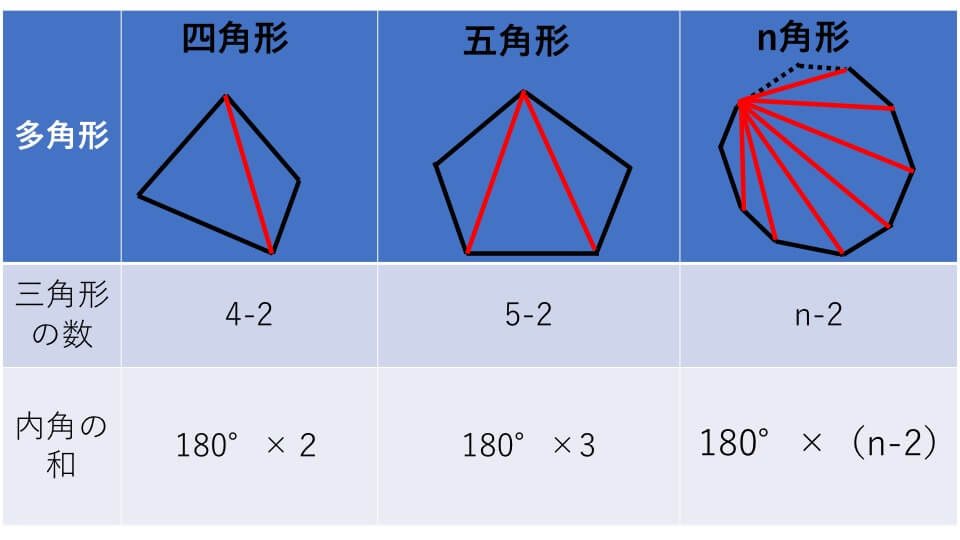
(1)三角形の内角の和と外角の定理を利用して、三角形の角の大きさを求めましょう。まず、内角と外角とは何か学んでいきましょう。 三角形の内角の和は、全ての 多角形 たかっけい の角度を求めるときの基礎です。八角形(はっかくけい 、はちかくけい、はちかっけい、はっかっけい)とは、8つの直線で囲まれた多角形 。 8個の頂点と8本の辺で構成される多角形のこと。 八辺形(はちへんけい)ともいう 。 八角形、および、八角形の構造体を、英語では "octagon" といい 、日本語でもその音写形である 多角形(四角形・五角形・六角形・・・)の内角の和の公式&問題の解き方 管理人 10月 6, 18 / 11月 18, 18 そしてその中でもさらに多角形の内角の角度に関する問題は頻出されます。
1
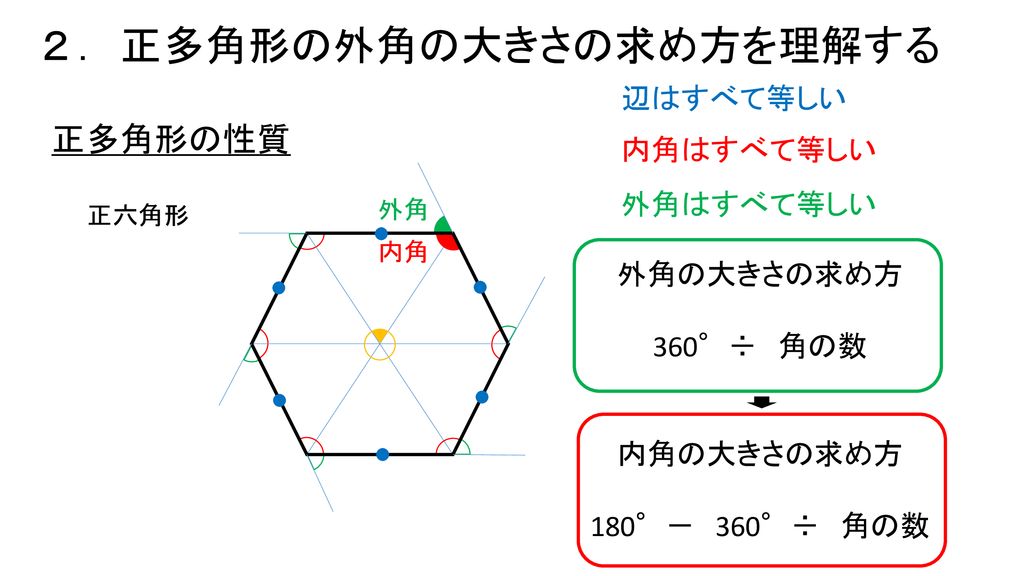
多角形の角の求め方
多角形の角の求め方-五角形や六角形を調べる際も、児 童自ら「三角形や四角形の内角の和が使えそうだ」と予想を立てながら考えさせる。自分が調べ て角の大きさの和が分かった図形を基にして、「どんな多角形でも求められる」という児童の姿を 引き出したい。 (2)児童観多角形の内部の任意の2点を結ぶ線分がその多角形の内部に含まれる ような多角形を凸多角形(convex polygon)という. この定義では対象となる2点対が無限に存在するので,計算不可能. 性質1:多角形Pが凸多角形であるための必要十分条件は,Pのすべての
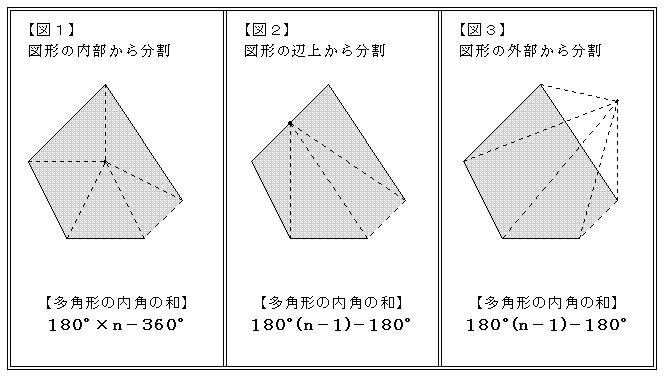



多角形の角
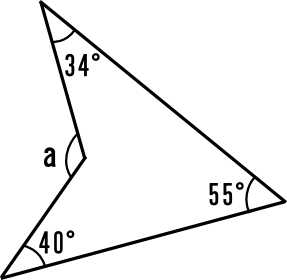
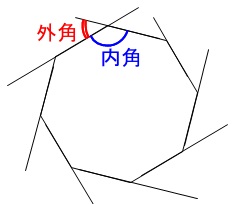
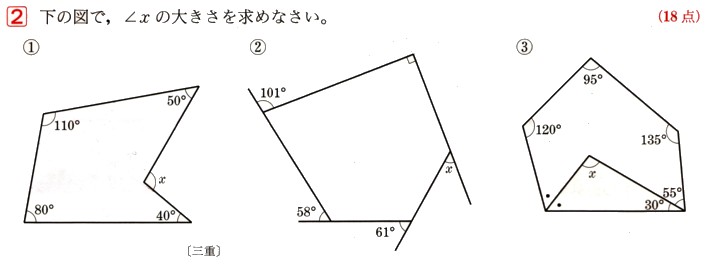
添付画像の黒い印の角の角度の和を求めたいのですが 形が複雑で 求め方が分らず困っています。 解答は540°です。 教えていただけると大変助かります。 宜しくお願いします。小学校5年生 算数 図形の角 多角形の角の大きさの和の求め方 学校図書通常の多角形は2次元の凸状の形をしていて、長さの等しい辺と角度の等しい角で構成されています。 四辺形や 三角形 は簡単な公式で面積を求めることができるものの、辺の数が5つ以上の多角形の面積を求めるのであれば、その形状の辺心距離 と外周をを用いた方が良いでしょう。
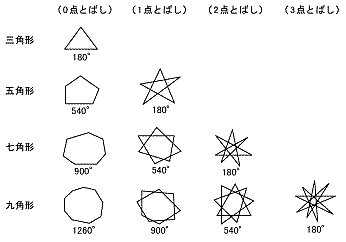
知多角形の外角の和を求めるいろいろな方法を理 解している。 2/2 (本時) ・やや複雑な図形の角度を求める。 ・星形多角形の先端の角の和を求め ることを考える。 思いろいろな多角形の角の求め方について論理的 に推論を進めようとしている。形六角形と 同じになる。 3番目ごと に結んだ星 形七角形と 同じになる。 3番目 ごと かくことが できない。 かくことが できない。 4番目 ごと 点の結び方 星形五角形 星形六角形 星形七角形 星形八角形 星形九角形星形十角形 角の和の公式 単位:度(°)角度の表し方(復習) 図1の赤で示した角は半直線baとbcでできている。 このba、bcを角の辺といい、点bを 角の頂点 という。
中2数学「多角形の角」の問題 どこよりも簡単な解き方・求め方 今回は「多角形の角」を学習します 基本的なところは算数で学習しましたね 「三角形の角の性質」「多角形の内角(外角)の和」「へこみのある図形の角度」について一緒に見ていきましょう課題学習の指導(数学) 1. 教材 「星形多角形の内角の和を追究しよう」(2年) 2. 教材観 三角形や多角形の内角の和を学習した後で,発展問題としてよく扱われる教材である。 星形五角形だけとっても,その形のきれいさで生徒の興味・関心を 下の図で色を塗った部分の多角形(七角形)の外角の和は360°になるので、 ● の和が360°、また ● の和も360°となります。 問題の印をつけた部分の和は三角形7つ分の内角の和- (● の和+ ● の和) となり、180°×7-360°×2= 540° となります。




正多角形の内角を4秒で計算できる公式 Qikeru 学びを楽しくわかりやすく



3分で分かる 多角形の内角の和の求め方 公式の証明などをわかりやすく 合格サプリ
多角形の頂角の和を求めてみよう。」という前時の課題を発展させて、 星形多角形の頂角の和について調べてみよう。 色々な星形多角形を作図し、頂角の和を求めなさい。 どんな求め方がありますか。またいどんなことに気がつきますか。・星形六角形の頂角の和は,ほとんどの生徒が求めている。 <発表された生徒の解き方> (4) レポート作成の課題を与える。 1) 頂角の和が180度になる星形多角形を調べよう。 2) 星形偶数多角形の性 直角三角形の底辺と高さから傾斜角 と斜辺 汎用の収納box(ベンチストッカー)を斜面に置く時の足の延長な為に継ぎ足す六角 直角の出し方




中2数学 正多角形の外角の大きさが3秒でわかる公式 Qikeru 学びを楽しくわかりやすく




多角形の角度の和の求め方 添付画像の黒い印の角の角度の和を求めたいのです Okwave
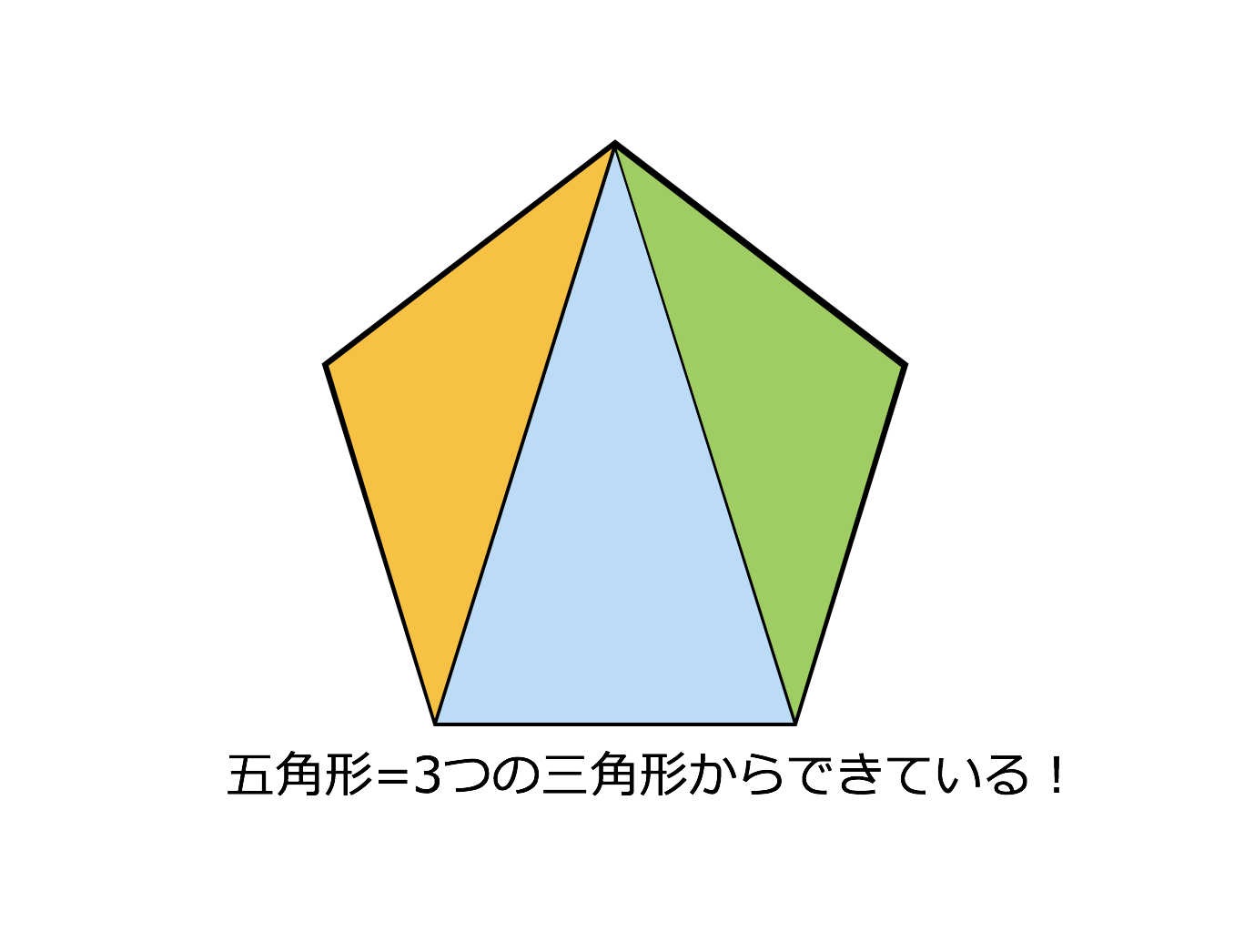
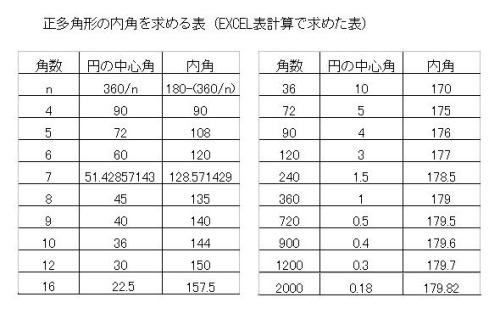
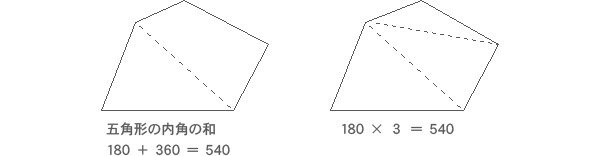
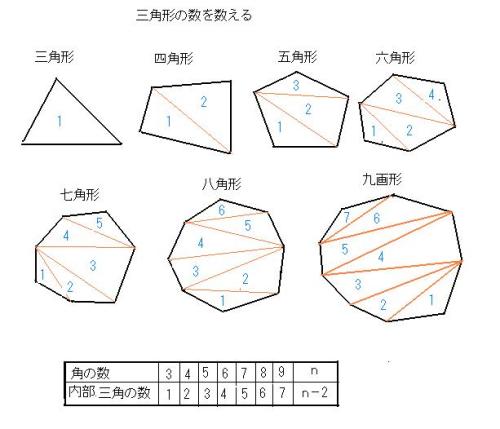
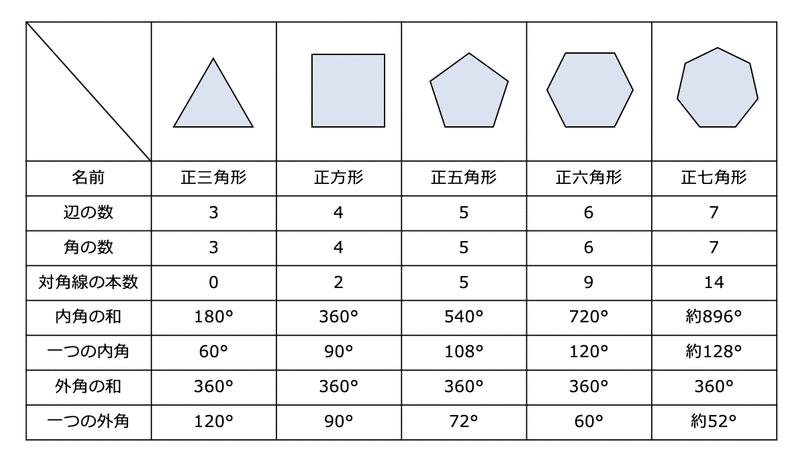
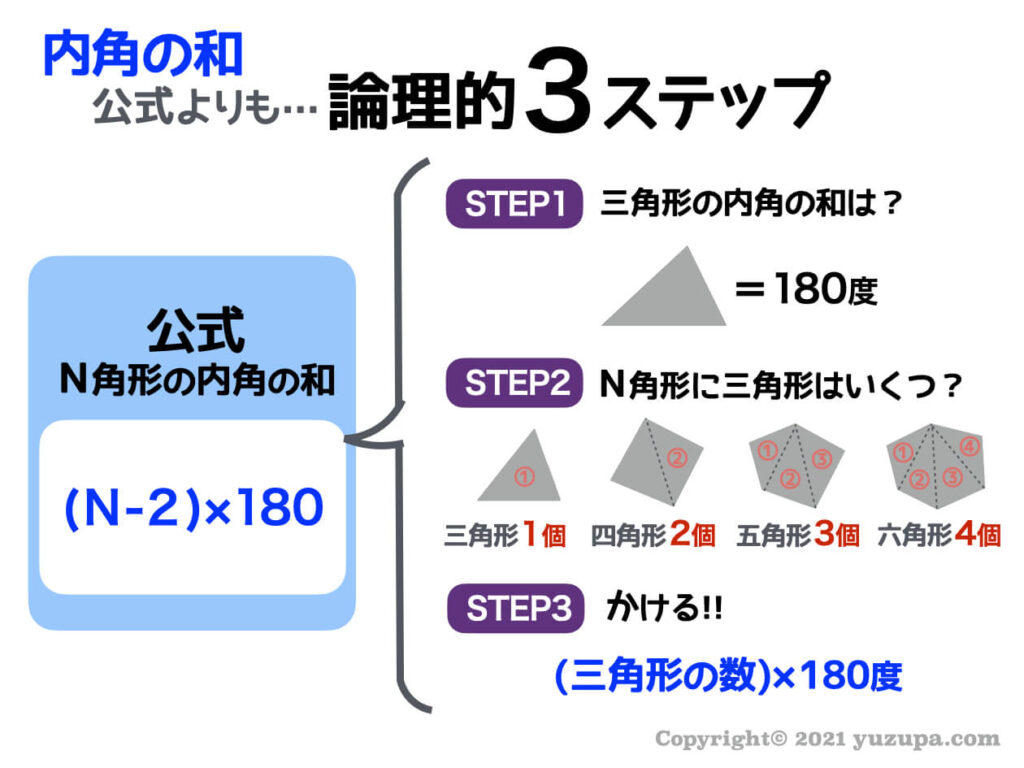
②正多角形のかき方 ③円周率の求め方(円の円周と直径の関係) ④円周や直径の求め方 ⑤生活の中で円周を求めるよさ 教え方1 正六角形や正八角形を作らせながら、正六角形や正八角形の意味をとらえさせます。 動画を見せて六角形のつくり方を説明し、 三角形の数は(52=3)で求めることができます。 三角形の内角の和は180°なので、五角形の内角の和は、180°×3=540° になります。 多角形の角の性質を下の表にまとめました。必ず覚えてください。この表を理解することで、どんな多角形が来ても内角の和を 選んだ角とそれの隣の角を除くと、角が 5 つ残りますが、 選んだ角から、その 5 つの角に線を引きます。 その結果、正八角形が 6 つの三角形に分割されます。 正八角形の内角の和は、 6 つの三角形の内角の和の合計に等しいですから、 180×6 = 1080° になります。 1つの角の角度は 1080÷8 = 135° になります。



正多角形の1つの内角 外角を求める方法を問題解説 数スタ




図で覚える多角形の外角の和の公式 Irohabook
3<π<4の証明 の流れを汲んで $\pi$ の値を求めることを考える。 基本的には \ (\text{内接多角形の周}) < (\text{円周}) < (\text{外接多角形の周}) \ の不等式に基づいて多角形の角の数を多くすることで $\pi$ を上下から挟みこむ方針である。円周率の求め方 home> ピンポイント解説>円周率の求め方 多角形による円周率の近似 正多角形の角の数を増やしていくと、形が円に近付いていく。 次の図では、角の数を6から24に増やすだけで、かなり円に近付くことがわかる。 多角形の面積の求め方 長方形=縦×横 正方形=1辺×1辺=対角線×対角線÷2 平行四辺形=底辺×高さ 台形=(上底+下底)×高さ÷2 ひし形(対角線直交四角形)の面積=対角線×対角線÷2 三角形=底辺×高さ÷2 円の面積の求め方



8ページ目の記事一覧 多面体紙工作で数学を楽しむ 行動の記録 楽天ブログ



重なる形と図形の角を調べよう 第5学年 小学校 算数 My実践事例 日本文教出版
正多角形の内角・外角の求め方を解説!←今回の記事 星形の角度の求め方を解説! ブーメラン型の角度の求め方! ちょうちょ型の角度の求め方を解説! 合同な図形の基本性質とは? 三角形の合同条件を使って、合同な三角形を見つける方法!正多角形の内角・外角の求め方を解説! 星形の角度の求め方を解説!←今回の記事 ブーメラン型の角度の求め方! ちょうちょ型の角度の求め方を解説! 合同な図形の基本性質とは? 三角形の合同条件を使って、合同な三角形を見つける方法!こんにちは、ウチダです。 今日は、中学2年生で習う 「多角形・正多角形の角度」 について、まずは多角形の内角の和・外角の和を考察し、次に正多角形の一つの内角・外角の求め方を考察します。 証明や練習問題なども扱っていますので、ぜひご覧ください♪ 多角形の内角の和・外角の和
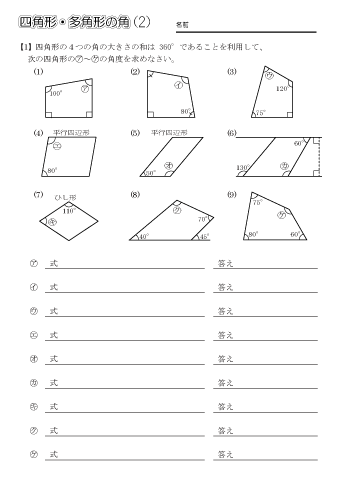



小学5年生の算数 四角形 多角形の角 問題プリント ちびむすドリル 小学生




分かりません 教えてください Clear
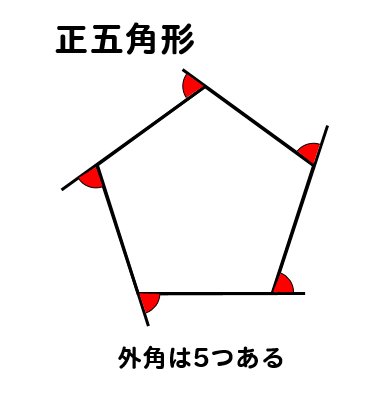
Ⅰ 面積の公式 以前の記事で、正三角形から正六角形までの面積の求め方を紹介しました。(「正多角形の面積の公式」を参照) 今回は、正 \(~n~\) 角形の面積、つまり一般化してみたいと 多角形の内角の和は公式つかえばドヤ顔できるけど、 せ、正多角形の内角はどうすれば・・・?? ってなるよね。 そんな流れで、 正多角形の内角の求め方 を解説していくよ。 よかったら参考にしてみてね^^ 4秒で計算できる!正多角形の内角の公式 三角形だろうが、六角形だろうが、百角形だろうが! どんな多角形であっても外角を全部集めて足すと360°になります。 次は、 隣り合う内角と外角の和は180°になる ということです。 「隣り合っている=直線になっている」



多角形の内角の和は 1分でわかる公式 問題の求め方 簡単な証明




中学2年生 多角形の内角外角 公式 個別進学教室マナラボ受験 教育情報サイト




内角の和 180 N 2 外角の和 360 教遊者




正多角形の内角を4秒で計算できる公式 Qikeru 学びを楽しくわかりやすく




3分で分かる 多角形の内角の和の求め方 公式の証明などをわかりやすく 合格サプリ




多角形の角



720度 星形九角形の角度の和




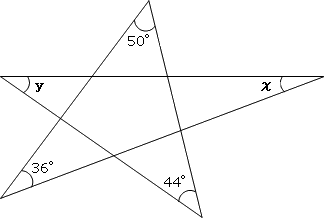
角度の求め方 算数の教え上手 学びの場 Com




小5 算数 小5 31 三角形の角 Youtube



問題1 平行線に二本の直線が交わっているとき Xの大きさを求めよう




多角形の内角の和 は何度なのか を説明します おかわりドリル



課題学習の指導 数学



数学教育 幾何 図形 的見方 多角形
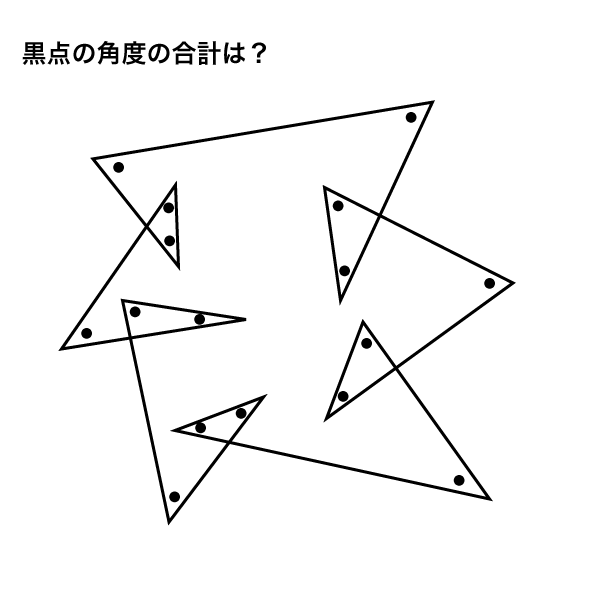



角度情報がない図形の合計の角度 星形多角形 受験算数入門



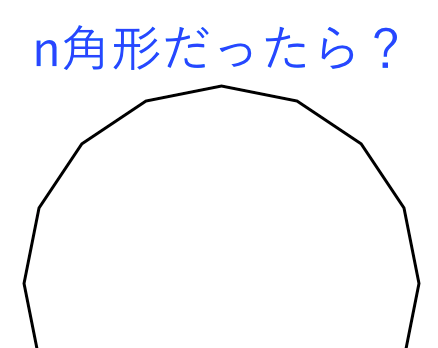
n角形 多角形 の内角の和の求め方



多角形の外角の和は360度 をgifアニメで表現 これがわかりやすいと海外で話題に 19年5月22日 エキサイトニュース
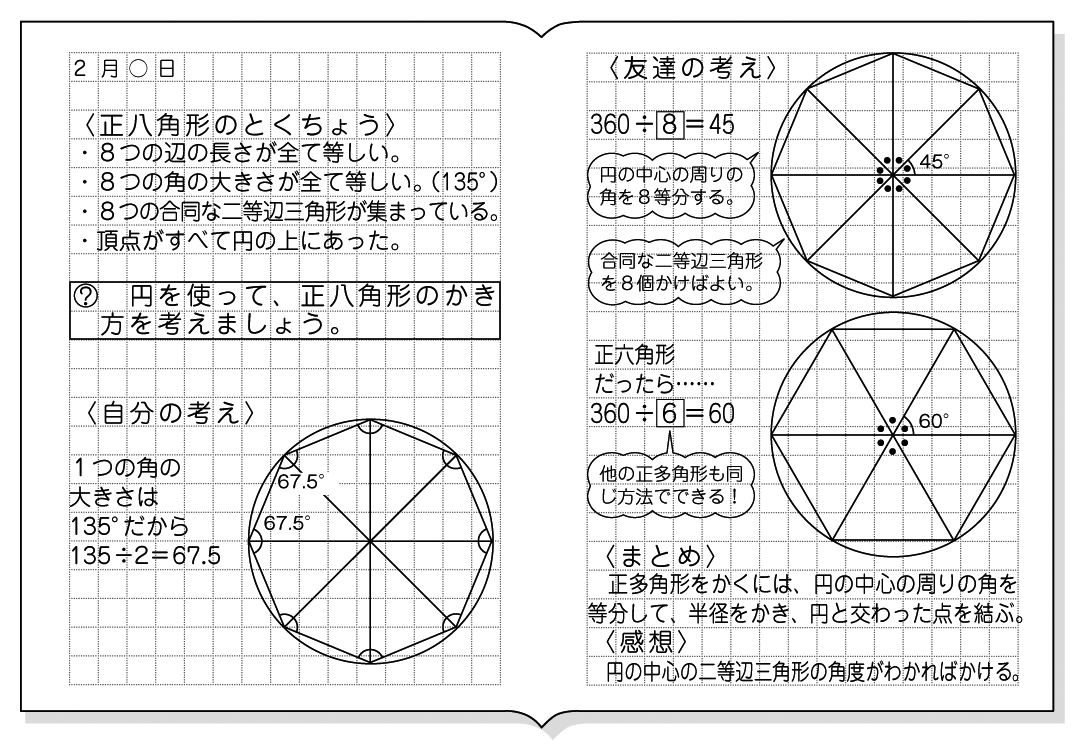



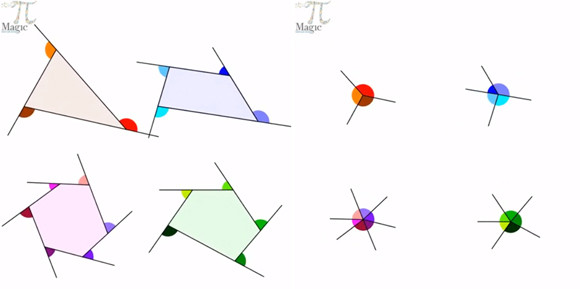
小5算数 正多角形と円 指導アイデア みんなの教育技術



正8角形です あ い う それぞれの角度の求め方を教えてください 一つの角の Yahoo 知恵袋




小学4年生 角度の求め方は 対頂角 平行線 同位角 錯角 中学受験 そうちゃ式 受験算数 2号館 図形 速さ




多角形の内角の和 は何度なのか を説明します おかわりドリル




3分でわかる 多角形の外角の和の求め方 Qikeru 学びを楽しくわかりやすく




多角形の内角の和 外角の和は 正多角形の内角の求め方は 証明や問題をわかりやすく解説 遊ぶ数学




3分でわかる 多角形の外角の和の求め方 Qikeru 学びを楽しくわかりやすく
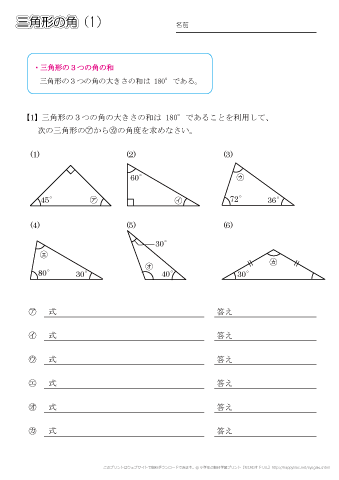



小学5年生の算数 多角形の角 三角形の角 問題プリント ちびむすドリル 小学生
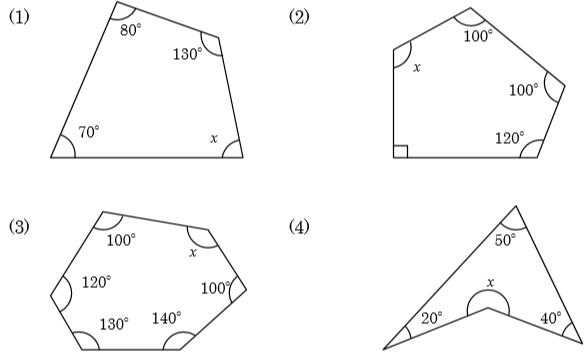



中2数学 多角形の内角の和と外角の和のポイントと練習問題 Pikuu



正多角形の作図 プログラミングで多角形を描く方法を考えよう 1時間目 Ppt Download




小学校5年 算数 正多角形の角の大きさ Youtube



正多角形の作図 5年生 算数の広場



多角形の内角と外角 思考力を鍛える数学



角度の求め方 算数の教え上手 学びの場 Com
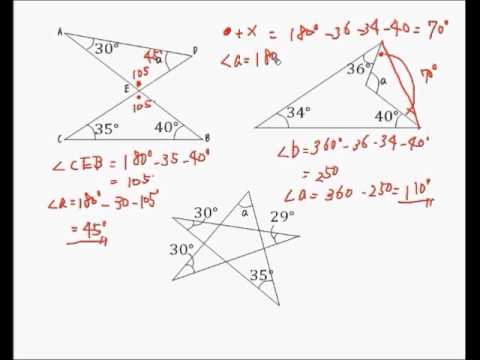



多角形から角を求める Youtube




中2数学 多角形の内角 外角 図形の合同 ひっそりと物理や数学を解説する



多角形とは 外角 内角の和 面積 対角線の本数の公式と求め方 受験辞典
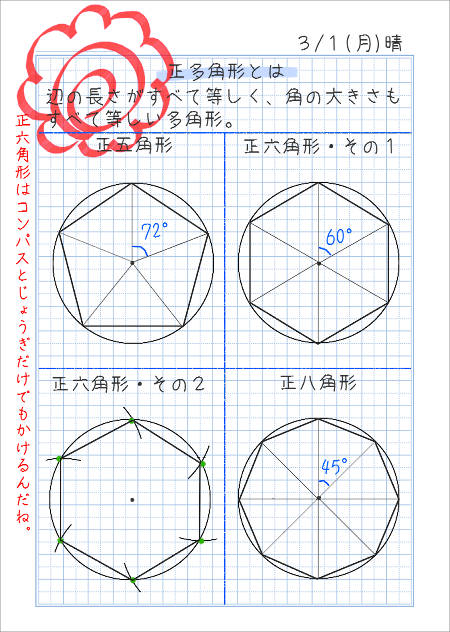



いろいろな正多角形をかいてみよう 家庭学習レシピ




正多角形の 内角が あっという間に分かる術 名寄 算数数学教室より



数学 の記事一覧 多面体紙工作で数学を楽しむ 行動の記録 楽天ブログ




星型 角形の角度の問題 恋する中学受験 大学受験を見据えた中学受験




内角の和 180 N 2 外角の和 360 教遊者



Q Tbn And9gctqxnxegjdxp Adpruavnpmf2sansioyhqkmwlqdbcw Fiiw67x Usqp Cau




内角の和 180 N 2 外角の和 360 教遊者
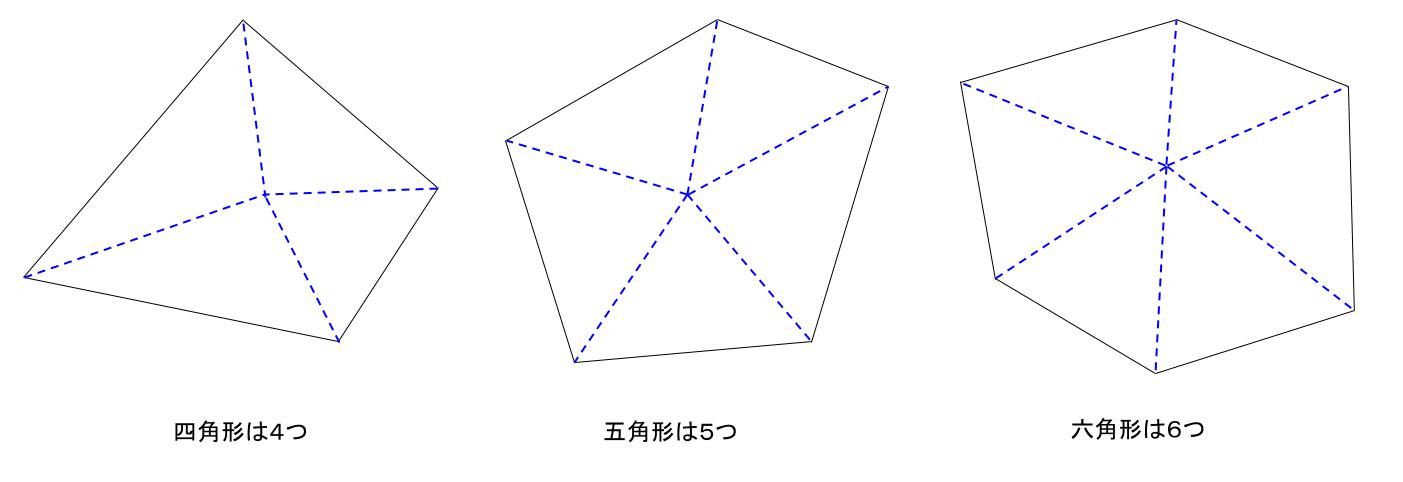



中学数学 多角形の内角 外角 中学数学の無料オンライン学習サイトchu Su
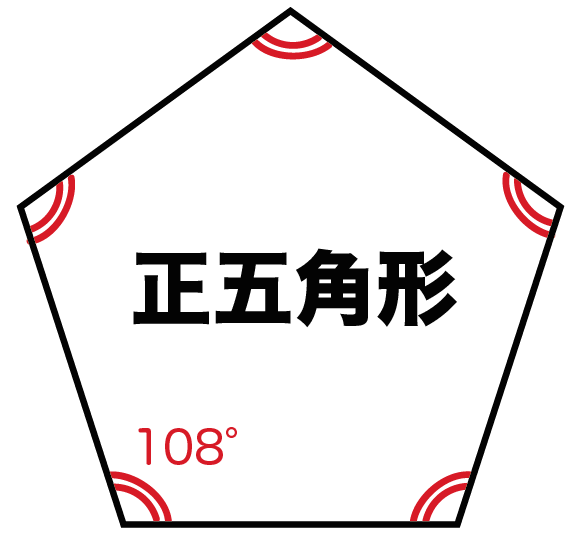



正多角形の内角を4秒で計算できる公式 Qikeru 学びを楽しくわかりやすく
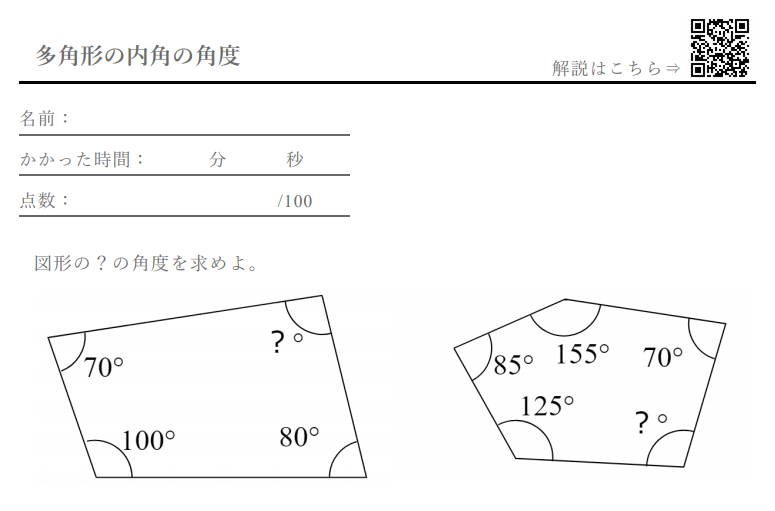



多角形 の内角の角度 計算ドリル 問題集 数学fun



ペンタゴンの秘密 正五角形の謎を解く 空間情報クラブ 株式会社インフォマティクス
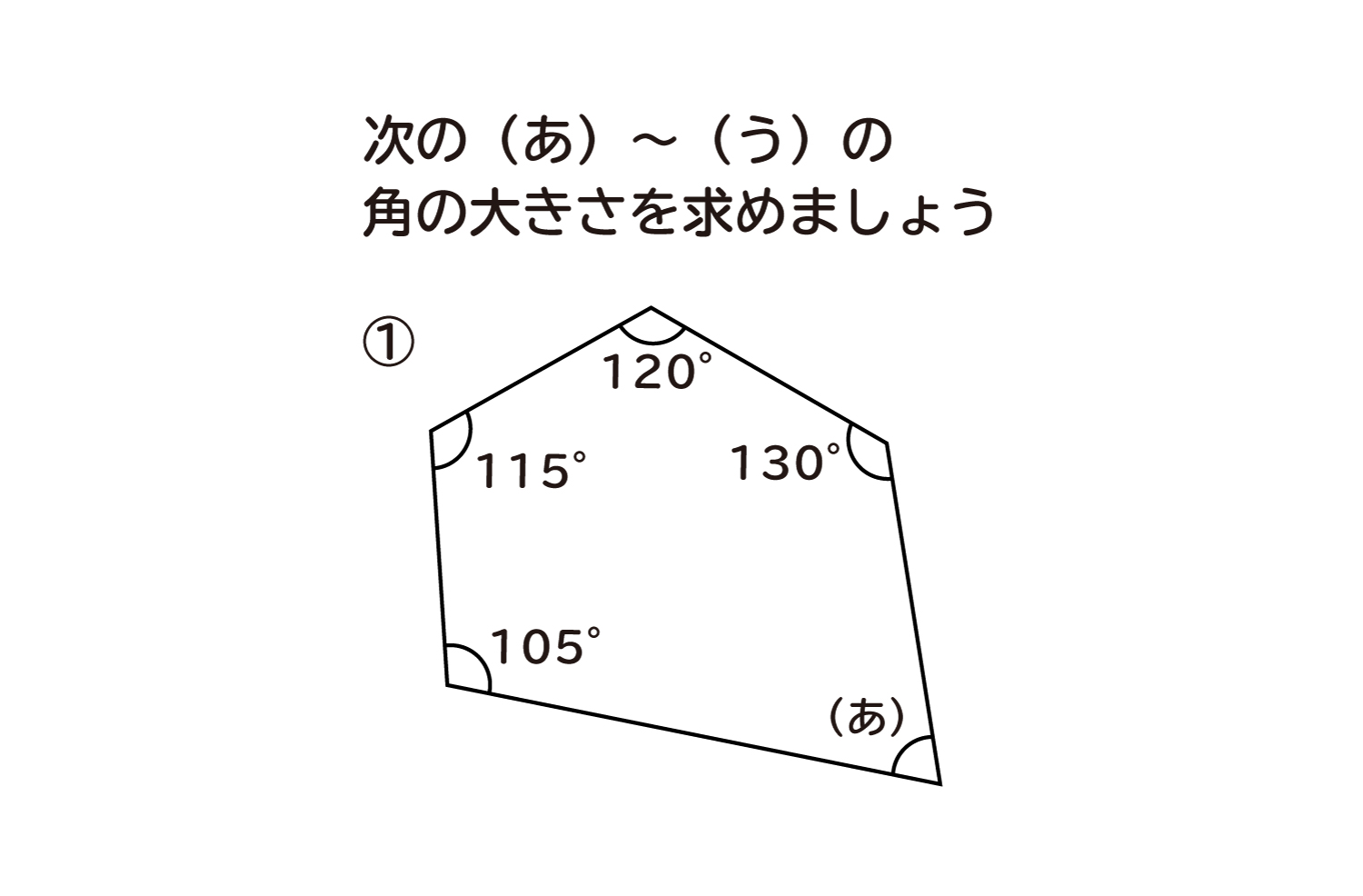



小学5年生 算数 無料問題集 多角形の角の大きさ おかわりドリル
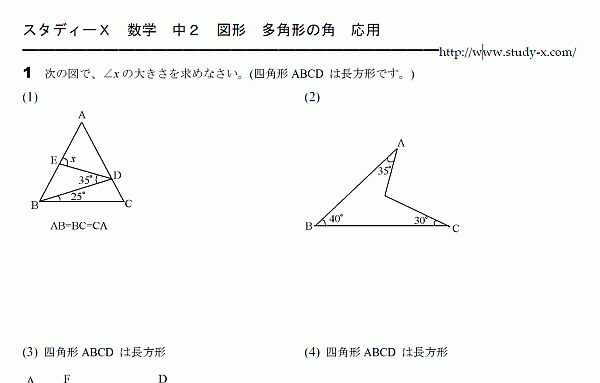



多角形の角 応用 無料学習プリント教材
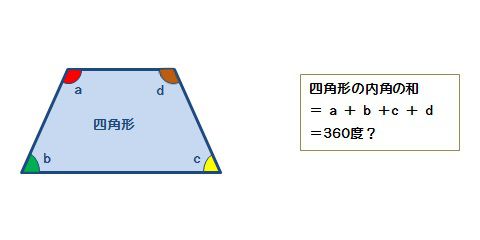



四角形の内角の和 算数の公式覚えてますか




正多角形の内角を4秒で計算できる公式 Qikeru 学びを楽しくわかりやすく




分かりません 教えてください Clear



中学受験 算数 角度 基礎からわかりやすくポイント解説 中学受験アンサー




複雑な多角形の角度の和が知りたいのですが 添付画像の16か所の黒丸部分の Okwave




多角形の内角の和 算数の公式覚えてますか




多角形の内角の和 外角の和の公式 数学fun




中2数学 ブーメラン型角度の求め方を解説 数スタ




多角形の角 無料で使える中学学習プリント



Studydoctor多角形の角度の問題 中2数学 Studydoctor



1



中学2年数学練習問題 図形の調べ方 多角形の内角と外角の解答



実践例 プログラミングで正多角形を学ぶ 山崎智仁 Tomohito Yamazaki Note



図形の調べ方 N角形について 内角の和を求める 苦手な数学を簡単に




多角形の内角の和の公式を3通りの方法で証明する 具体例で学ぶ数学
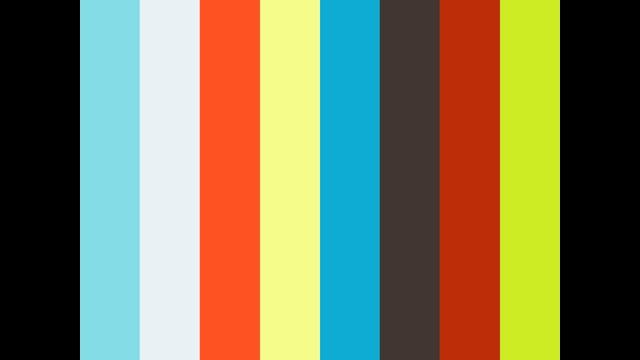



2 48 第3章 多角形の角 いろいろな図形の角 Kakera Link 公式ブログ




多角形の内角の和の求め方をイチから解説するぞ 中学数学 理科の学習まとめサイト




多角形の外角の求め方を5分でサクッと理解 中学数学 理科の学習まとめサイト



なぜ星型七角形の角の和は540 になるのでしょうか 中2でも分か Yahoo 知恵袋



多角形の内角の和の公式と外角の和を利用した角度の求め方
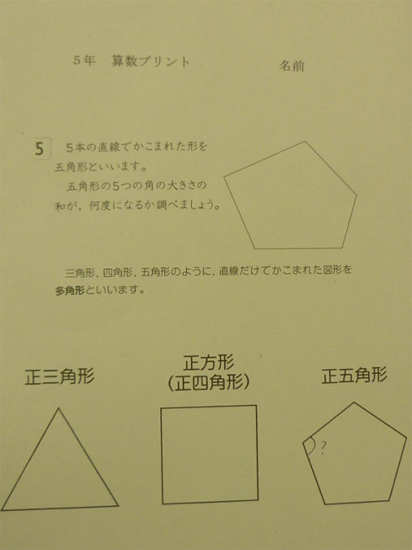



重なる形と図形の角を調べよう 第5学年 小学校 算数 My実践事例 日本文教出版




中2数学 複雑な多角形 角の和 応用問題
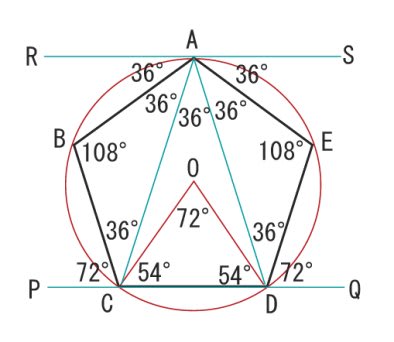



正五角形というだけで 分かる角度は 名寄 算数数学教室より
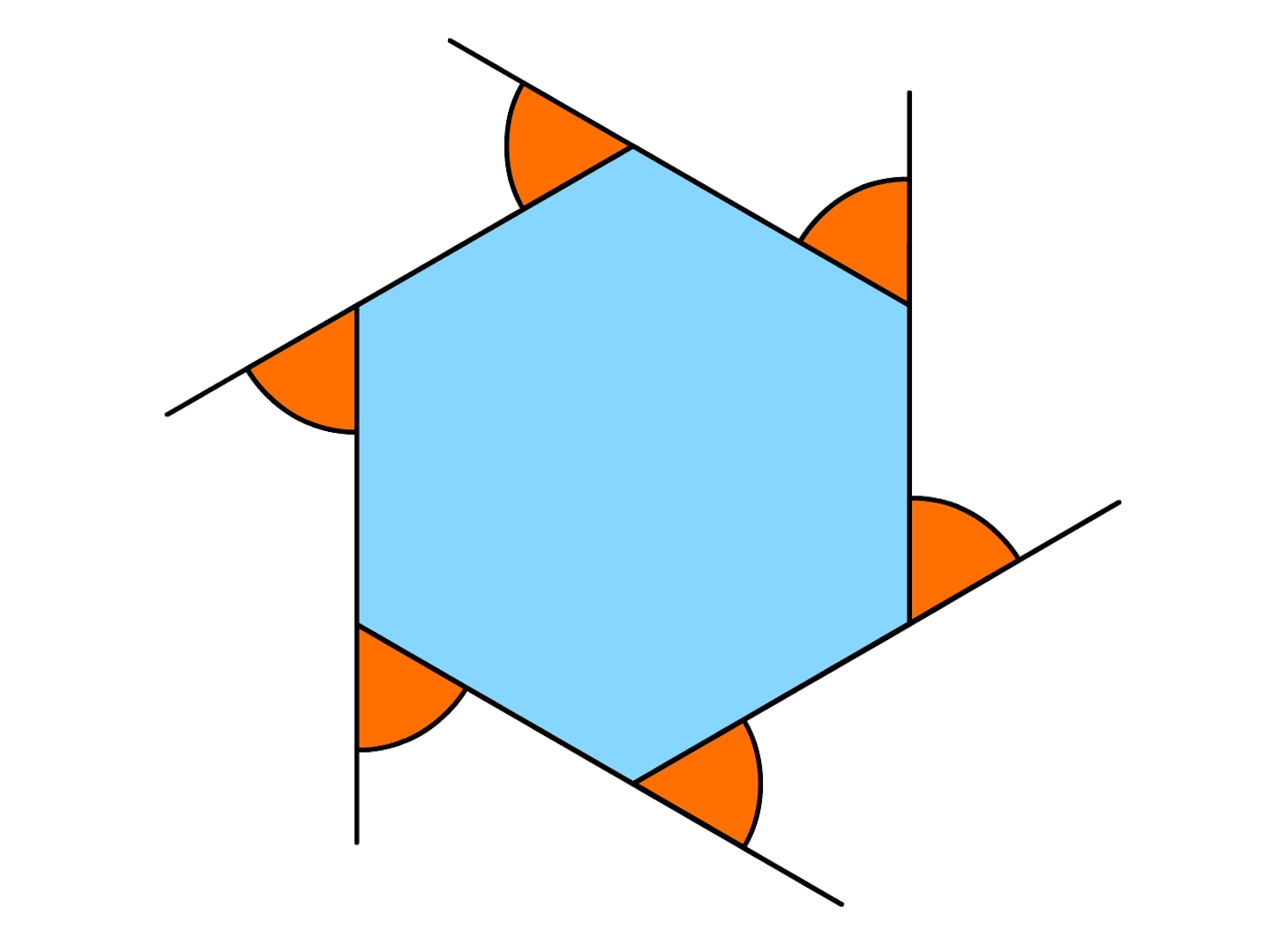



2年 多角形の外角 数学イメージ動画集 大日本図書




正多角形の内角と外角の大きさ 具体例で学ぶ数学




多角形の内角の和 一覧表と簡単公式による求め方 Yattoke 小 中学生の学習サイト
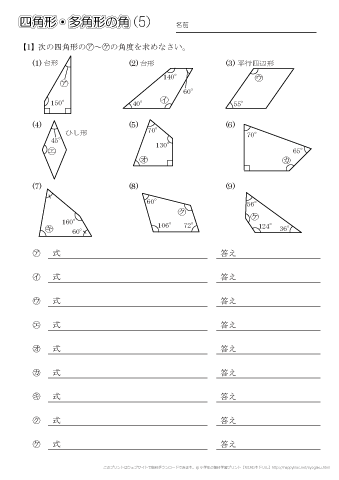



小学5年生の算数 四角形 多角形の角 問題プリント ちびむすドリル 小学生
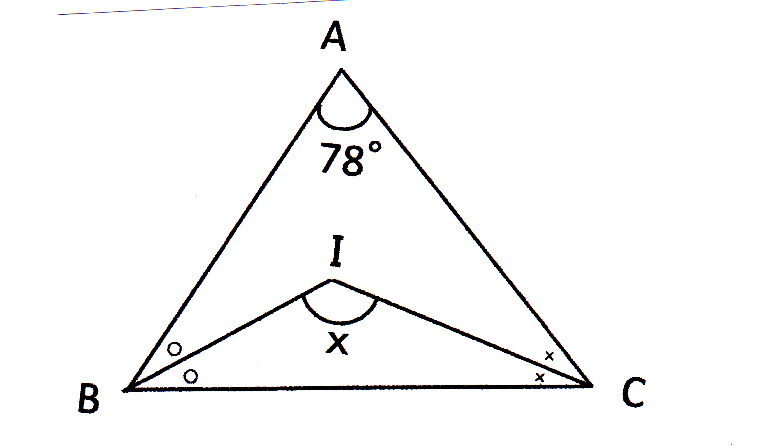



図形 角度 錯角 同位角 多角形の内角外角など 現役塾講師のわかりやすい中学数学の解き方




中2数学 複雑な多角形 角の和 応用問題
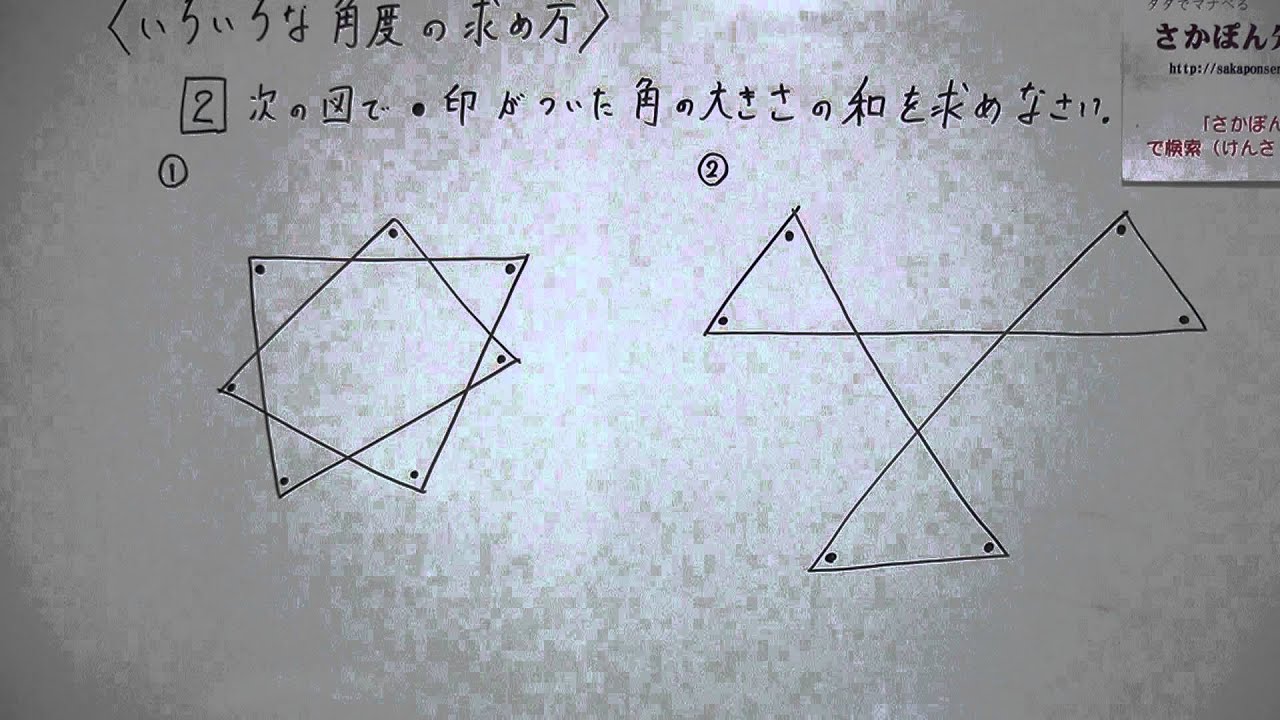



中学校2年生数学 いろいろな角度の求め方
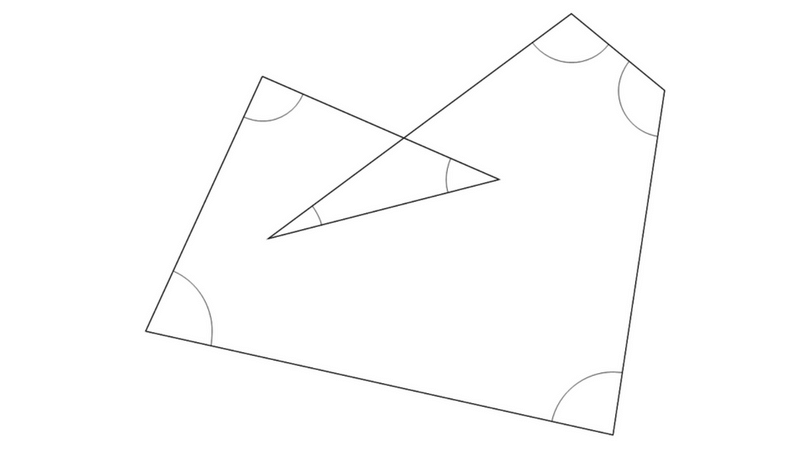



数学の図形で使えるスリッパの法則を使って星の角度の和をだそう まぜこぜ情報局




内角の和 算数用語集
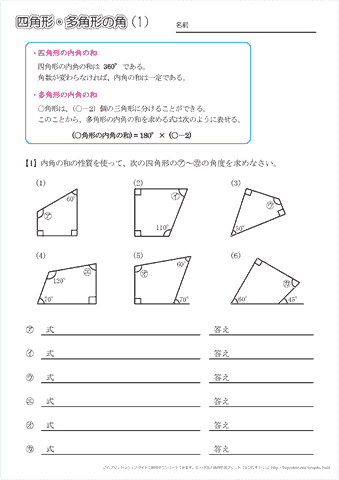



小学5年生の算数 四角形 多角形の角 問題プリント ちびむすドリル 小学生




数学 中2 51 多角形の内角と外角の和 基本編 Youtube




いろいろな正多角形をかいてみよう 家庭学習レシピ
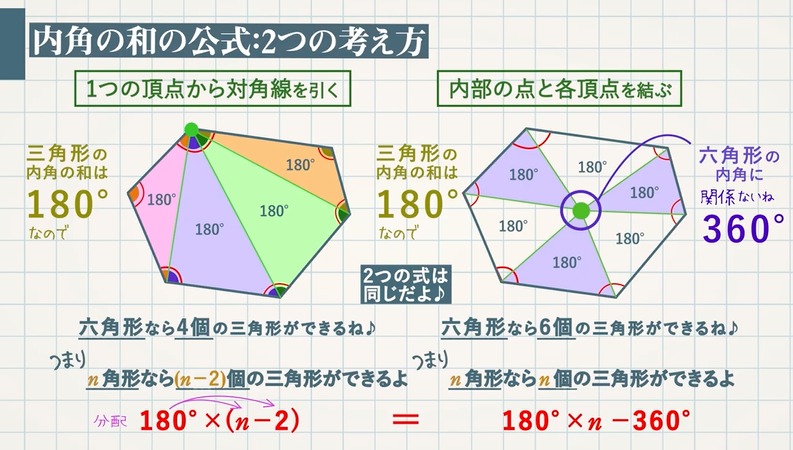



内角の和 180 N 2 外角の和 360 教遊者




多角形 四角形 五角形 六角形 の内角の和の公式 問題の解き方 数学fun




多角形の内角の和の公式を3通りの方法で証明する 具体例で学ぶ数学



1
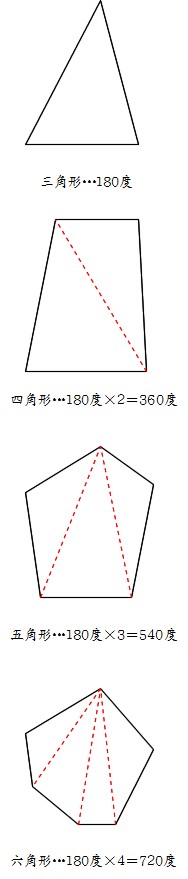



Math 多角形の内角の和 働きアリ




内角の和の公式 内角の和が1800 の多角形は何角形 中学や高校の数学の計算問題



小5 算数 小5 33 多角形の角 Youtube



1



中学2年数学 図形の調べ方 三角形 多角形と角 確認問題2 解答 あんのん塾




多角形とは 内角の和の求め方を簡単に解説 高校生向け受験応援メディア 受験のミカタ




多角形の内角の和と外角の和 三角形や四角形 五角形の角度 リョースケ大学




課題学習の指導 数学



中学受験 多角形の内角の和 公式を忘れなくする論理的3ステップ かるび勉強部屋



0 件のコメント:
コメントを投稿